Apparent Motion Laboratory

Dr. Robert Goldstone
Psychology Department/ Cognitive Science Program

Indiana University

This laboratory explores the phenomenon of apparent motion. When still frames are rapidly alternated, people often spontaneously perceive motion. By studying apparent motion phenomena, we can learn about how people subjectively structure the external world , the assumptions that people make about stimuli when perceiving, top-down effects in vision, and the specific mechanisms that people use to see motion. Apparent motion is also an indispensible to the motion picture industry because movies are nothing more than a series of still frames that are rapidly displayed.

The computer program for apparent motion does two things. First, it allows you to create and display apparent motion phenomena. You can design an apparent motion display, and then present it to yourself and determine the motion that you spontaneously see. Second, it provides a computational model of how people see apparent motion. Typically, you will use this program by presenting the same apparent motion display to yourself and to the computational model, and observing whether the computer "sees" the same kind of motion that you do.

The program allows you to draw two static frames, and then alternates them in a manner specified by experimenter-controlled parameters. The program does not collect any data from the subject; there are too many possible data that might be collected. In many cases, the effects are so strong and immediately obvious that experimenters can use their own impressions as data, and can be fairly confident that other people will see the displays in the same way. This lab is designed to have quite a bit of flexibility. The experimenter can create their own displays with different geometric shapes, each with its own color and size.

The "Motion Correspondence Problem"

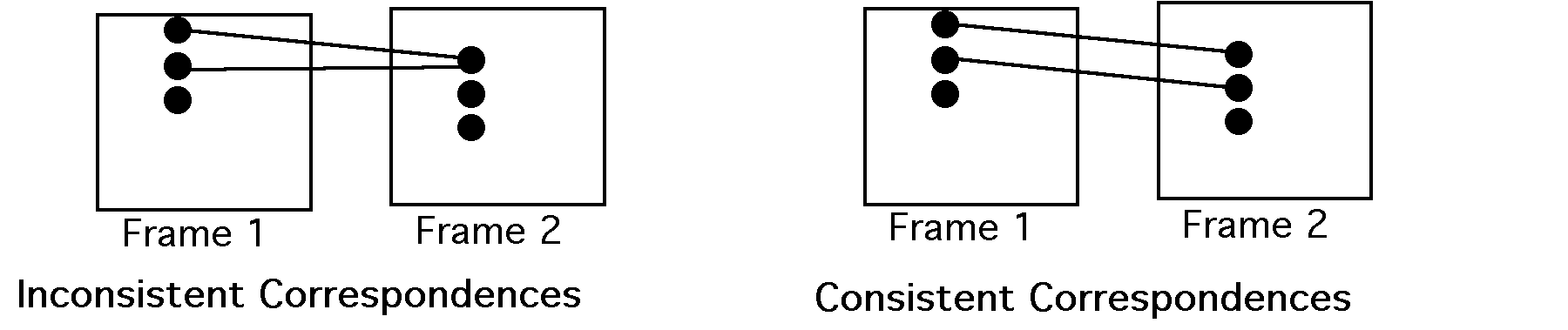
When people see motion between two successively presented frames, their minds unconsciousnly determine which parts from the first frame correspond to which parts from the second frame. When people see two parts as corresponding to each other, this means that they interpret the two parts as coming from the same object. If the two parts are separated from each other, then people will see a single object moving over time.

Determining what parts correspond to each other tells us what parts come from the same object at different times. However, this task is intrinsically ambiguous. One part in one frame could correspond to many different parts in the other frame. Simple experiments will show that people sometimes see two parts as showing the same object moving over time even if the parts do not have the same color, size, location, or even shape! Your mind spontaneously figures out what parts correspond to each other, but underlying this seemingly effortless feat are sophisticated computations. Your mind uses several constraints in order to try to determine what parts correspond to each other. Constraints are valuable, not restrictive things to be avoided, because without constraints the world is too ambiguous. Constraints allow us to restrict our perceptions to the most plausible possibilities.

Assumptions That Solve the "Motion Correspondence Problem"

Imagine that there are two frames, each with three circles. Each object from one frame might correspond to any of the three objects from the other frame. Your mind makes assumptions about what objects are likely to belong together:

1. Proximity: Your mind assumes that objects appearing at two different times are really the same object if they are close to each other.
   Shape, size, and color similarity: Your mind assumes that objects appearing at two different times are really the same object if they are similar in their shape, size, and color.
2. Motion similarity: When two objects are placed in correspondence, a direction of motion is specified between them. Your mind assumes that all of the objects in a display move in similar directions.
3. One-to-one mapping constraint: All else being equal, your mind tries to match up objects so that each object in one frame has ONE AND ONLY ONE corresponding partner in the other frame.

All of these constraints act together to determine the motion that you will in a display. None of these constraints is hard and fast. Your mind can often times overrule these constraints, but they are biases that generally lead people to see motion in a reasonable manner. Impressively, all correspondences between all objects are determined at the same time, and the correspondences mutually influence each. The last two assumptions above make this clear. Whether or not an object corresponds to another object depends on all of the other objects and THEIR emerging correspondences.

Experimental Exploration of Apparent Motion
While exploring the human perception of apparent motion, you may want to try out some of the following displays:

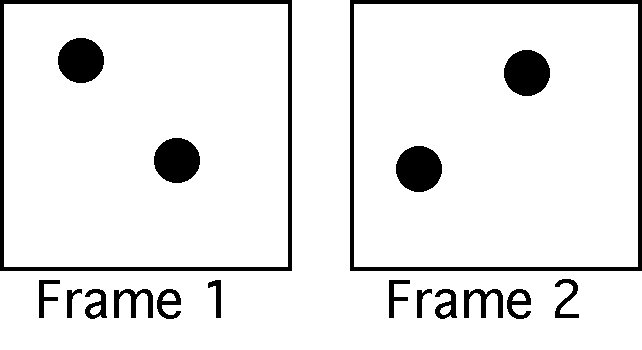
Notice here that you will most likely either see two dots sliding up and down, or two dots sliding left and right. You can see either of these effects by selectively hiding pairs of dots and gradually constrained so that every dot in one frame corresponds to one and only one dot in the other frame.

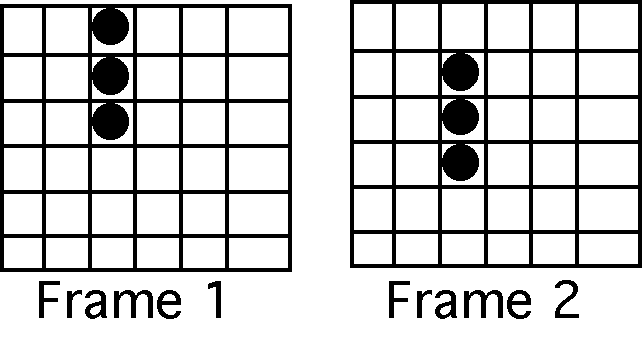This is called the "Ternus Display." The grid is displayed to show you the precise locations of dots. If there is a short blank period between these frames, people typically report seeing three dots moving up and down. This is suprising because some of the dots have EXACTLY the same location in the two frames, and yet people don't see them as stationary. People DO see them as stationary if there is no blank period between frames. What do you think is going on here (HINT: remember the one-to-one mapping constraint)?

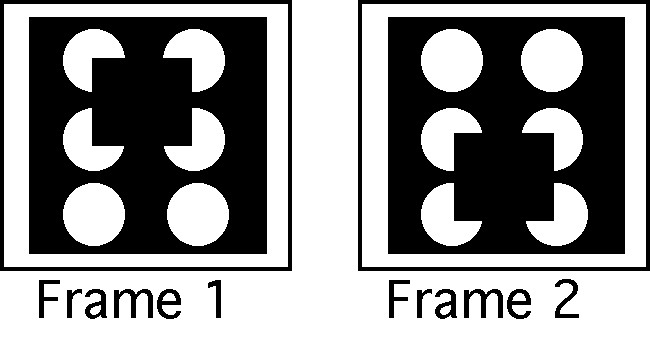This display can be created with the program although it will require a bit of ingenuity. It combines two illusions: illusory contours (seeing a complete black square even though there are only white "pac-man" shapes) and illusory motion. What do you see when these displays are alternated? What does your perception imply about whether your mind creates illusory contours BEFORE or AFTER it creates apparent motion?

Computational Modeling of Apparent motion

The computer simulation is a simple neural network that has been designed to implement the assumptions/constraints previously described. In this network, one unit is created for every potential correspondence between two objects. If two frames each have 3 objects in them, 9 units will be created because each of three objects in one frame can correspond to three objects from the other frame. Each unit has an activation, and the more active the unit is, the more strongly the computer "feels" that the two objects connected by the unit should be placed in correspondence. In the simulation, the activity of a correspondence unit is shown by the amount of green in the connection between objects. In accordance with the described constraints, the following principles govern thechange in a unit's activity over time:

1. Location, color, shape, and size similarity: Correspondence units will tend to be active if the objects they connect have similar positions, colors, shapes, and sizes. The importance of each of these kinds of similarity can be controlled by the user.
2. One-to-one mapping constraint: Correspondence units will tend to become deactivated if they are inconsistent with other highly active correspondence units. Correspondences are inconsistent if they would place TWO objects from one frame in correspondence with ONE object from the other frame.Match: If an object has no correspondending partner, then it will appear to blink on and off. Correspondences will tend to develop so that every object has at least one corresponding partner.
   
3. Motion similarity: Correspondence units will tend to become active if the direction of motion that they indicate is similar to the directions of motion indicated by other highly active correspondences.
   

The neural network begins with all correspondences' activations set to zero. Then, the units gradually change their activations by the above principles, and as they do so, they will change other units' activations.

Using the Laboratory Software

When you run the program, you will see a screen that contains a description of Frame 1 and Frame 2. The first thing you will want to do is create the two frames that will make up the animation. To do this, you can select from three different shapes (square, circle, and diagonal line) and three different sizes. You can also color the object in many different ways by selecting the amount of red, green, and blue in the color using the three color sliders. To paint objects on the frames, press the paint button and click on the spot in the frame where you want the object to appear. The appearance of the object will be determined by the color, shape, and size that you have selected. To erase an object, press the erase button and click on the object that you wanted deleted. To move an object, press the move button, and then click on the object you want to move, and drag it to its new location. To copy an object from one frame to the other, press the copy button and click on the object you want copied. Press clear if you want to erase all of the objects, flip to turn on/off the animated alternation of the two frames, and grid if you want a grid to (dis) appear on the screen that can help you position objects. Press info to find out more information about how to use the program. If you want to save two frames that you created, press the save button and select a file name. You can load in previous files that you created by pressingthe load button.

While the two frames are flipping, no button or slider can be altered. You break out of flipping mode by pressing the mouse button. While the two frames are flipping, each will appear on the screen for a period of time that you determine by selecting a value on the slider called duration. There may also be a time period between each frame during which the screen is blank. You specify how long this time period is by selecting a value on the blank time slider.

In addition to the above buttons and sliders, there are other sliders that you will need to use if you are interested in exploring the computational model of human apparent motion perception. The sliders color, size, and shape determine how much the neural network bases its correspondences between the two frames on each of these properties. The consistency slider specifies how much the model tries to enforce the one-to-one mapping constraint. The motion similarity slider specifies how much the model tries to have objects move in similar directions. The match slider specifies how hard the model tries to find a partner for each object. For each of these parameters, as you move the slider value to the right, the parameter has a greater influence on how the neural network. The speed slider determines how quickly correspondences are determined, and the randomness slider specifies how much randomness is added to correspondence units' activity.

The computational model is turned on/off by pressing the model button. When the model is turned on, a set of correspondence units is created, one unit for each possible connection between objects across the two frames. Each correspondence unit starts with zero activity. On each time step, the activity of a correspondence unit changes, based on the parameters that you specify. The strength of a correspondence unit is indicated by its green hue. The computer predicts that objects connected by bright green lines will be perceived as coming from the same moving object.

The ghost button allows you to see where an object from one frame would appear if it were on the other frame. It will appear as a hollowed-out object on the other frame. If ghost is turned on and the modeling is on, then rather than drawing correspondences between objects across frames, the computer will draw correspondence from the objects of one frame to the ghosts of the objects in the other frame.