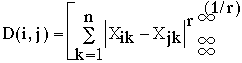Goldstone, R. L. (in press). Similarity. in R.A. Wilson & F. C. Keil (eds.) MIT encyclopedia of the cognitive sciences. MIT Press: Cambridge, MA.

Assigned Length: 1000 words

Actual Length: 1193 words

Address correspondences to:

Dr. Robert Goldstone

Psychology Department

Indiana University

Bloomington, IN. 47405

rgoldsto@ucs.indiana.edu

An ability to assess similarity lies close to the core of cognition. In the time-honored tradition of legitimizing fields of psychology by citing William James, "This sense of Sameness is the very keel and backbone of our thinking " (James, 1890/1950; p. 459). Similarity plays an indispensable foundational role in theories of cognition. People's success in problem solving depends on the similarity of previously solved problems to current problems. Categorization depends on the similarity of objects to be categorized to category members. Memory retrieval depends on the similarity of retrieval cues to stored memories. Inductive reasoning is based on the principle that if an event is similar to a previous event, then similar outcomes are predicted. An understanding of these cognitive processes requires that we understand how humans assess similarity. Four major psychological models of similarity are: geometric, featural, alignment-based, and transformational.

Geometric models have been among the most influential approaches to analyzing similarity (Torgerson, 1965), and are exemplified by multidimensional scaling (MDS) models (Nosofsky, 1992; Shepard, 1962). The input to MDS routines may be similarity judgments, confusion matrices (a table of how often each entity is confused with every other entity), probabilities of entities being grouped together, or any other measure of subjective similarity between all pairs of entities in a set. The output of an MDS routine is a geometric model of the entities' similarity, with each entity of the set represented as a point in N-dimensional space. The similarity of two entities i and j is taken to be inversely related to their distance, D(i,j), which is computed by

,

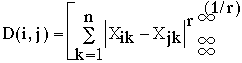where n is the number of dimensions, Xik is the value of dimension k for entity i, and r is a parameter that allows different spatial metrics to be used. A Euclidean metric (r=2) often provides good fits to human similarity judgments when the entities are holistically perceived or the underlying dimensions are psychologically fused, whereas a City-block metric (r=1) often provides a better fit when entities are clearly divisible into separate dimensions (Garner, 1974). Shepard (1987) has made a compelling case that cognitive assessments of similarity are related by an inverse exponential function to distance in MDS space.

Geometric models standardly assume minimality [D(A,B) ³ D(A,A) = 0], symmetry [D(A,B) = D(B,A)], and the triangle inequality [D(A,B)+D(B,C) ³ D(A,C)]. Tversky (1977) criticized geometric models on the grounds that violations of all three assumptions are empirically observed. Minimality may be violated because not all identical object seem equally similar; complex objects that are identical (e.g. twins) can be more similar to each other than simpler identical objects (e.g. two squares). Asymmetrical similarity occurs when an object with many features is judged as less similar to a sparser object than vice versa; for example, North Korea is judged to be more like China than China is to North Korea (Tversky, 1977). The triangle inequality can be violated when A (e.g. "lamp") and B ("moon") share an identical feature (both provide light), and B ("moon") and C ("ball") share an identical feature, but A and C share no feature in common (Tversky & Gati, 1982). Although geometric models can be modified to correct these assumptions (Nosofsky, 1991), Tversky suggested an alternative approach, the Contrast Model, wherein similarity is determined by matching features of compared entities, and integrating these features by the formula

S(A,B) = q f(A«B) - a f(A-B) - b f(B-A).

The similarity of A to B, S(A,B) is expressed as a linear combination of the measure of the common and distinctive features. The term (A « B) represents the features that items A and B have in common. (A-B) represents the features that A has but B does not. (B-A) represents the features that B, but not A, possesses. The terms q , a , and b reflect the weights given to the common and distinctive components, and the function f is often simply assumed to be additive. Other featural models calculate similarity by taking the ratio of common to distinctive features (Sjoberg, 1972).

Neither geometric nor featural models of similarity are well suited for comparing things that are richly structured rather than just being a collection of coordinates or features. Often times, it is most efficient to represent things hierarchically (parts containing parts) and/or propositionally (relational predicates taking arguments). In such cases, comparing things involves not simply matching features, but determining which elements correspond to, or align with, one another. Matching features are aligned to the extent that they play similar roles within their entities. For example, a car with a green wheel and a truck with a green hood both share the feature green, but this matching feature may not increase their similarity much because the car's wheel does not correspond to the truck's hood. Drawing inspiration from work on analogical reasoning (Gentner, 1983; Holyoak & Thagard, 1989; see ANALOGY), in alignment-based models, matching features influence similarity more if they belong to parts that are placed in correspondence, and parts tend to be placed in correspondence if they have many features in common and if they are consistent with other emerging correspondences (Goldstone, 1994; Markman & Gentner, 1993).

A fourth approach to modelling similarity is based on transformational distance. The similarity of two entities is assumed to be inversely proportional to the number of operations required to transform one entity so as to be identical to the other (Hahn & Chater, 1997; Imai, 1977). For example, "XXXXO" requires only one transformation to become "XXXOO" (change an O to an X), but requires two transformations to become "OOXXXX" (change an O to an X, and reverse string), and consequently is more similar to "XXXOO."

All four approaches have enjoyed some success in quantitatively predicting people's similarity assessments, and testing between these models' approaches to comparing entities is a major, ongoing topic of research. Another major issue concerns the role of similarity in other cognitive processes. For example, while several models of categorization are completely similarity-based (see CONCEPTS), other researchers have argued that people's categorizations cannot be exhaustively explained by similarity but also depend on abstract, theoretical knowledge (Rips & Collins, 1993; Murphy & Medin, 1985). Another complication to the explanatory role of similarity is that similarity may not be a unitary phenomenon. Similarity assessments are influenced by context, perspective, choice alternatives, and expertise (Medin, Goldstone, & Gentner, 1993; Tversky, 1977). Different processes for assessing similarity are probably used for different tasks, domains, and stimuli. The choice of features, transformations, and structural descriptions used to describe entities will govern the predictions made by similarity models as much as do the models' mechanisms for comparing and integrating these representations. History has not supported a literal interpretation of Fred Attneave's (1950, p. 516) claim, "The question 'What makes things seem alike or seem different?' is one so fundamental to psychology that very few psychologists have been naive enough to ask it" in that the topic has inspired considerable research, but this research has vindicated Attneave at a deeper level by testifying to the importance and complexity of similarity.

Attneave, F. (1950). Dimensions of similarity. American Journal of Psychology, 63, 516-556.

Goldstone, R. L. (1994). Similarity, interactive activation, and mapping. Journal of Experimental Psychology: Learning, Memory, and Cognition, 20, 3-28.

Hahn, U., & Chater, N. (1997). Concepts and similarity. In L. Lamberts & D. Shanks (eds.) Knowledge, Concepts, and Categories. Hove, U.K.: Psychology Press/MIT Press.

Imai, S. (1977). Pattern similarity and cognitive transformations. Acta Psychologica, 41, 433-447.

Markman, A. B., & Gentner, D. (1993). Structural alignment during similarity comparisons. Cognitive Psychology, 25, 431-467.

Nosofsky, R. M. (1991). Stimulus bias, asymmetric similarity, and classification. Cognitive Psychology, 23, 94-140.

Rips, L.J., & Collins, A. (1993). Categories and resemblance. Journal of Experimental Psychology: General, 122, 468-486.

Shepard, R. N. (1962) The analysis of proximities: Multidimensional scaling with an unknown distance function. Part I. Psychometrika, 27, 125-140.

Sjoberg, L. (1972). A cognitive theory of similarity. Goteborg Psychological Reports, 2(10).

Torgerson, W. S. (1965). Multidimensional scaling of similarity. Psychometrika, 30, 379-393.

Tversky, A., & Gati, I. (1982). Similarity, separability, and the triangle inequality. Psychological Review, 89, 123-154.

Garner, W. R. (1974). The processing of information and structure. New York: Wiley.

Gentner, D. (1983). Structure-mapping: A theoretical framework for analogy. Cognitive Science, 7, 155-170.

Holyoak, K. J., & Thagard, P. (1989). Analogical mapping by constraint satisfaction. Cognitive Science, 13, 295-355.

James, W. (1890/1950). The principles of psychology. Dover: New York. (Original work published 1890)

Medin, D. L., Goldstone, R. L., & Gentner, D. (1993). Respects for Similarity. Psychological Review, 100, 254-278.

Murphy, G.L., & Medin, D.L. (1985). The role of theories in conceptual coherence. Psychological Review, 92, 289-316.

Nosofsky, R. M. (1992). Similarity scaling and cognitive process models. Annual Review of Psychology, 43, 25-53.

Shepard, R.N. (1987). Toward a universal law of generalization for psychological science. Science, 237, 1317-1323.

Tversky, A. (1977). Features of similarity. Psychological Review, 84, 327-352.