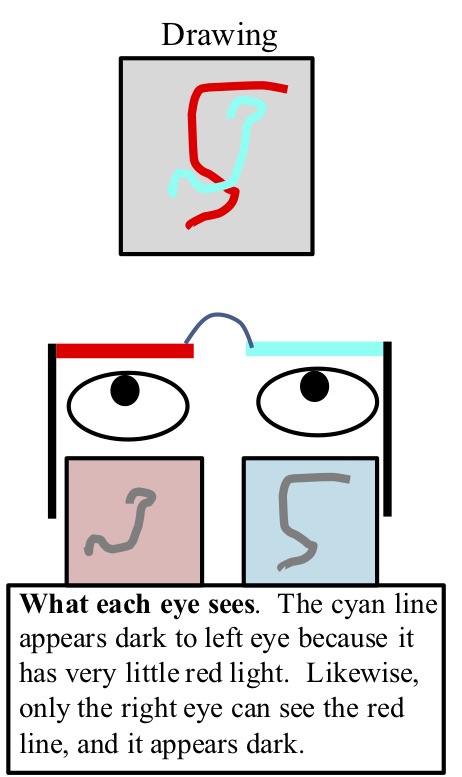
There are different ways of projecting different information to an observer’s two eyes. In many psychology and neuroscience laboratories,
liquid crystal glasses are employed that transmit different patterns of light selectively to the two eyes. A much cheaper and
readily available technology simply involves having observers wear glasses with different colored lenses. Imagine that a
red filter is in front of an observer’s left eye and a cyan (a combination of blue and green) filter is in front of their
right eye. The red filter will selectively allow red light to pass into the eye. A red image of equal luminance to a gray
background appears nearly invisible to the left eye because both the red image and the background have an equivalent amount
of red light that passes through the filter and this red light is the only light that passes through the filter. A cyan image
will appear darker than the background in the left eye because it contains very little red light and the background contains red,
blue, and green light. Accordingly, the left eye with the red filter will see cyan images as dark shapes while the right eye with
the cyan filter will see red images as dark shapes.
One felicitous side effect of using red-cyan 3D glasses to present different information to the two eyes is that the observer will
have a phenomenologically salient cue as to whether they are seeing their visual world with their left or right eye. Every patch
of their world, whether or not it contains an object, will appear tinted either red or cyan. If a patch appears to be red, then
this means that the observer is seeing that patch with their left eye, while cyan-tinted patches are being seen with their right
eye. These tints are subtle, lightly colored, and somewhat reminiscent of a halo. Normally, patterns of red- and cyan-appearing
patches will be highly structured in both time and space.
create some displays for yourself (including, perhaps, uniformly gray displays) and closely observe and report what you see. Some
specific suggestion for creating the report on what you see while wearing red-cyan glasses:
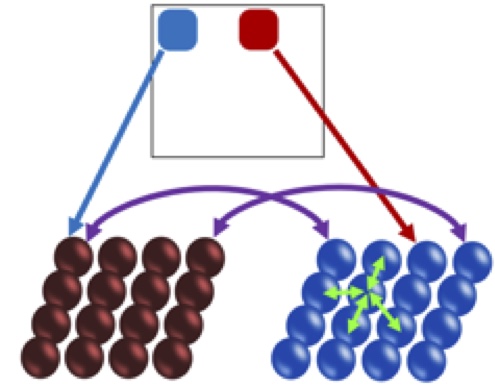
I have incorporated an interactive neural network organized as shown to the right. The image elements (a cyan and red blob) are
shown at the top, and below are two banks of neurons for the left and right eyes. I imagined that the neurons/units within a
bank are organized spatially in two dimensions, such that a cyan object in the upper left portion of the display would activate
the upper-left unit in the left eye (remembering that the cyan dot will be invisible to the eye with the cyan filter in front of it).
Strong activation of this left-eye unit would lead to the subjective impression of a reddish tint in this upper-left region of the space.
Fleshing out this model for me, then, amounted to specifying the kinds of excitatory and inhibitory relations between the units, as
exemplified by the purple and green arrows, adding some randomness to each unit’s activation at each moment, and postulating that units fatigue/habituate
over time to the extent that they are active. Some mechanism like habituation is needed so that once one eye become dominant in terms
of capturing awareness it eventually gives up control, allowing the other eye to become dominant. This alernation of eye dominance
is the hallmark of binocular rivalry.
When you press the "Run Model" button, you will see the moment-to-moment activations of each unit over time, as the units are influenced by
the external display and one another. Each unit is shown as a small box. Cyan and red units for the same location completely overlap each other.
The middle of the box shows what the external display's
color is at the location visible to the unit: gray, cyan, or red. The color of the square frame around a box shows the level of red and cyan unit activitations.
If the frame is strongly cyan, that means that the cyan unit for that location is highly active and the red unit is not active. This means that the model
is predicting that a human would be seeing that location with their right, cyan-tinted eye. So, typically, if a location in the display
is colored cyan, then it will be visible to left eye with the red filter on it, and this will tend to cause the red eye to become activated, and
so there will be a bright red box around the cyan-filled center.
In real time you can manipulate parameters underlying the behavior of the model:

